by Diogo Pires
Within any society, lives are not independent. From households to our workplace, from where we go to whom we meet, we constantly make decisions, implicit or not, which have an impact on others. Many of these decisions relate, for example, to how we split work or share resources between us. Under some scenarios our interests align, while in other cases conflicts emerge. We can then ask ourselves: what makes people collectively adopt any particular type of behavior in each of the social settings they are confronted with?
Using games to explain the spread of behavior
Picture a society where everyone behaves similarly, when all of a sudden, a single person decides to experiment and acts distinctly from everyone else’s. What determines whether that will be a successful new trend spreading throughout society, or an unsuccessful one succumbing to the established? Evolutionary game theory suggests the answers might be found by looking at this topic through the lens of games played within an adapting population. Every time people interact, we consider them to do it via a game that is defined by three features: the players, their possible actions, and the payoffs they receive depending on their actions. Game theory focuses on cases where the outcome of our encounters depends not only on our choices but on the combination between our choices and those of others.
Since we are interested in understanding emerging social behavior, we turn our focus from what each one of us does individually to what happens at the scale of our society. This is where evolutionary dynamics come into the stage. The payoffs of games are used to represent success in our interactions, whatever our measure of success is. Gaining higher payoffs makes individuals more successful in the population, leading others to imitate them more often.
Eventually, strategies that make individuals more successful might spread throughout the whole population.
Sharing Resources and Splitting Work
Let’s think about a specific game that is commonly referred to as the Hawk-Dove game. You and a colleague of yours are two huge fans of banana bread—if you are not, just consider getting into it for your own pleasure. Someone left a slice of it in the common area in your office and both of you are interested in grabbing that one single piece. The problem is: you might have to go through a fight to get it. If both of you are ready to fight you have a 50% chance of getting the slice, and 50% of just getting hurt, a cost that surpasses the potential benefit of getting it. If both just ask for the slice, then each will get it without a fight with a 50% probability, which would be a fair outcome. However, the ideal scenario in your own self-interest is to be ready to fight for it against someone that is not. In that case, you would get the slice with certainty and without the need to fight for it!
As you might have guessed, the dynamics of “who-gets-the-cake” have an impact outside your office!
This game is used to represent the exploration of any common resources that people have at their disposal. In biology, under which evolution has a whole distinct meaning, it helps understanding confrontation for resources, territory, and mates. That’s exactly where its name comes from. If, for instance, crabs are competing for a patch of territory, we call being ready to fight a Hawk strategy, while fleeing and searching for other territories is called a Dove strategy.

How we split work that benefits or is needed by all has very similar dynamics and that’s where the alternative “Snowdrift” name to the same game comes from. When an access road has been blocked after a snowdrift, playing “Dove” is simply being ready to do the work, while playing “Hawk” is waiting for a neighbor to do it. In that case, the cost paid when both neighbors rest is the cost of not seeing the work done by anyone.
The decisions that we see in this game are often made repeatedly, either because resources are scarce or because there is a lot of work to do. Therefore, if you have a 50% chance of getting the cake, you will get it half of the times you meet. The main question is which sort of behavior do we expect to see evolving in groups where everyone meets, and how does their size affect this? Is fighting-till-death the inevitable catastrophe or will we see a fair split of resources? Do we expect exploitation by some, a production standstill, or a fair division of labor as societies become larger?
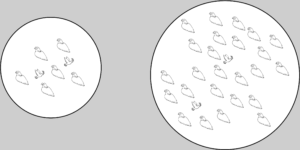
Larger societies can help the spread of new behavior, even in the absence of structure
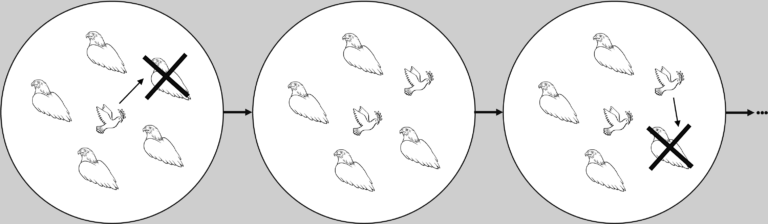
Let’s consider two societies differing only in their size. To become prevalent, any new differing strategist would have many more individuals whose behavior she would have to influence in the larger society. This suggests that the probability of success of her strategy could be lower in the case of a larger society, especially if there is not a social structure that amplifies the spreading of behavior. In fact, this is what happens if your success depends only on your strategy and not on that of others or, in other words, when we don’t need to use games to model the dynamics. However, when everyone’s actions are interdependent, as they are under the Hawk-Dove game, counter-intuitive phenomena emerge in the spread of new strategies.
We have found that being in a larger society is very often beneficial for a new single strategist. Most of the time, this happens if a new strategy does relatively better among the previously dominant behavior than it does among similar strategists. This is the case under the Hawk-Dove game. Let’s think about a population of Hawks where one single Dove appears. Being in a larger population means that initially, when Doves are the most vulnerable to disappearing because of their low numbers, both Hawks and Doves will interact more often with Hawks. Hawks won’t benefit from extorting many resources from Doves and they will pay the very high costs of fighting with other Hawks often.
Even though Doves will be extorted most of the time, they end up doing much better than Hawks simply by not engaging in the fights the Hawks constantly do. Because of this, Doves do better relative to Hawks in the most crucial part of the spreading process, assuring higher probabilities of fixating in larger populations
We noted that this happened under all games with two strategies where the best response to each of the strategies is always the opposing one – the anti-coordination games. The same effects were observed in other well-known games, such as the Prisoner’s Dilemma when Defectors do relatively better among Cooperators than they do among other Defectors.
Even though these results were surprising as they were, the phenomenon happens in rare ocasions when new strategies do relatively worse among previously established ones than they did among their own. These occurrences were observed when comparing small populations of different sizes. In these cases, all steps become important evolutionary steps due to the small size of the population, creating other overlapping effects. One surprising game in which this happened was the Stag-Hunt game, one of the so-called coordination games. We showed that fixation probabilities sometimes hold a maximum, which means that there is an optimal population size on which one cooperative Stag-Hunter could try to fixate.
A lot of work has been dedicated lately to studying how social connections and their structure influence the spreading of new information and behavior, some structures having been shown to amplify these processes and others to suppress them. By isolating the effects of population size, we were able to show that this alone can have striking counterintuitive results. They impact the way that several forms of fairness and cooperation evolves, as shown by their presence in games such as the Hawk-Dove, Prisoner’s Dilemma, and Stag Hunt game.
If you want to know more about the effects of population size on the fixation of strategies, you can find the paper with the exact account of these results (https://royalsocietypublishing.org/doi/abs/10.1098/rspa.2022.0577?af=R).