A brief history of analyzing stability of dynamical systems

by Mohammadreza Satouri

The first challenge after modeling a dynamical system like autonomous vehicles, aircraft, or cancer is analyzing the stability of that system. Different types of stability exist, like Lyapunov stability and input-output stability [1]. Roughly speaking, a system is Lyapunov stable if, for bounded initial states, we have bounded states all the time. Also, a system is input-output stable if it produces bounded output in response to a bounded input. For more details, you can look at [1]. In a more powerful case, the system becomes asymptotically stable if the states converge to some equilibrium. In this post, when we use the term stability, we mean asymptotic stability. If a system reaches unstable regime, this can lead to unwanted behaviour. For instance, if the velocity of a motor increases without limitation, it can damage the motor and surrounding devices. Thus, it is essential to analyze systems’ stability and make them stable using available controllers. In the sequel, we briefly look into the history of studying the stability of dynamical systems.

In 1840, Sir George Biddell Airy, a mathematician and astronomer, designed a velocity controller for a telescope to focus on a particular planet for a long time. When he saw severe fluctuations in his controller, he modeled the system and analyzed the fluctuations mathematically. He made the first effort to tackle instability in a closed-loop control system. He was also the first to use differential equations to analyze closed-loop control systems.

In 1868, James Clerk Maxwell used differential equations to analyze the stability of the fly-ball governors. He linearized the governor model and derived the characteristic equation of the system. He showed how the roots of the mentioned characteristic equation relate to the stability or instability of the system. He published his findings in the following paper, analyzing self-oscillation that can result in instability:

Maxwell, James Clerk (1868). “On Governors”. Proceedings of the Royal Society of London. 16: 270–283. doi:10.1098/rspl.1867.0055.

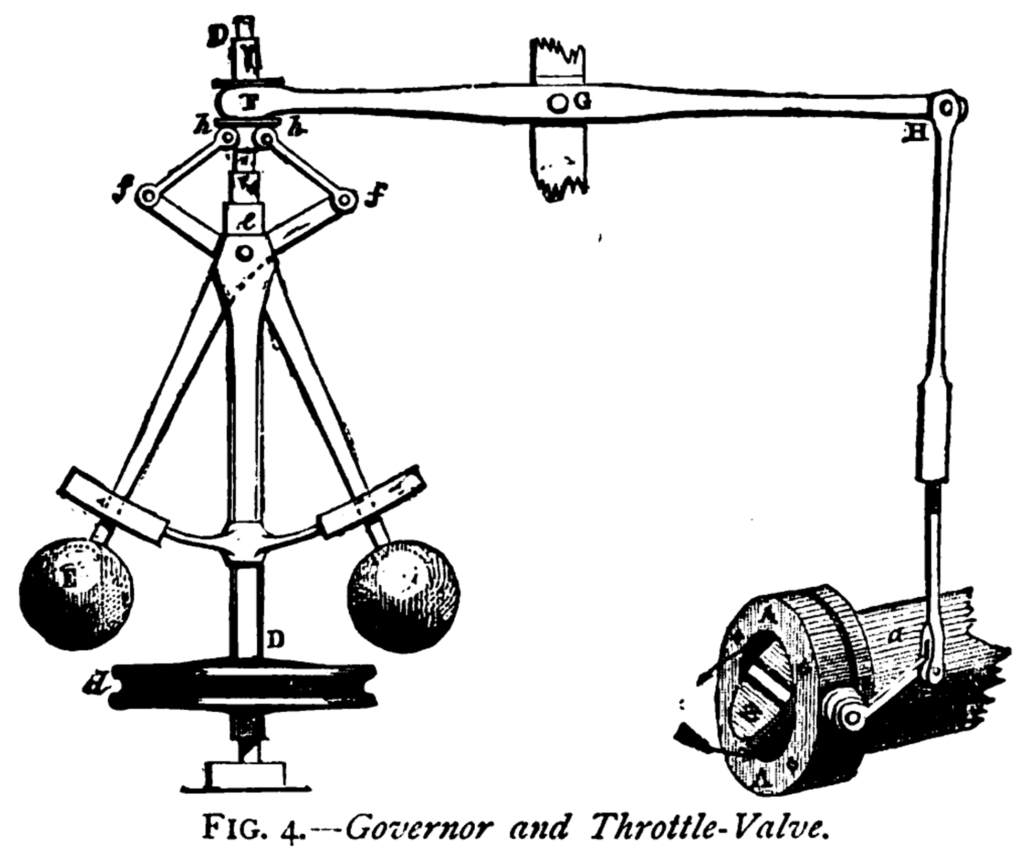
The method that Maxwell proposed can determine the stability of the systems of degrees less than four. Edward John Routh, an English mathematician, proposed an analytical method in 1877 that could determine the stability of systems of any degree. Because of this achievement, he received the Adams Prize, one of the most prestigious prizes awarded by the University of Cambridge.

French mathematician Charles Hermite developed a method in 1854 to analyze the roots of a general characteristic equation using quadratic terms. Afterward, German mathematician Adolf Hurwitz used Hermite’s results and found sufficient and necessary conditions for the stability of roots of characteristic equations. In 1895, Hurwitz found the relation between the roots of the characteristic equation and the stability of the corresponding linear system, independently of Routh, who had derived it earlier by a different method.

However, analyzing the stability of nonlinear systems was still a big challenge. Aleksandr Mikhailovich Lyapunov, a Russian mathematician and physicist, developed a stability theory in 1892, one of the biggest achievements in systems theory. He proposed two methods in his Ph.D. thesis: 1) Lyapunov’s indirect method (also called the first method of Lyapunov), which states that the stability of a nonlinear system can be determined by linearizing the dynamics around the equilibrium points. 2) The most famous one, Lyapunov’s direct method (also called the second method of Lyapunov), states that the stability of nonlinear systems can be determined by finding a Lyapunov function with specific properties. Although his methods greatly impacted Russian scientists, they were not translated into English until 1992. Since the importance of his methods was unknown until Rudolf Emil Kálmán, a Hungarian-American electrical engineer and mathematician, proposed designing controllers in the state space.

We saw how observation of fluctuations in a telescope controller motivated Sir George Biddell Airy to start mathematically analyzing that system’s stability. His work opened windows for more fundamental research in analyzing the stability of linear systems. Then Aleksandr Mikhailovich Lyapunov, in his Ph.D. thesis, proposed a brilliant method for analyzing the stability of nonlinear systems without explicitly solving the differential equations that describe the system. We can claim that the Lyapunov method is the most powerful method for analyzing the stability of general nonlinear systems so far. If you want more details about Lyapunov theory, you can look at the Nonlinear Systems book by Hassan K. Khalil [1].